树
- 二叉树
- 根节点, 左子节点, 右子节点
- 没有环
- 满二叉树
- 每个节点要么同时有左子节点和右子节点, 要么为叶子节点
- 完全二叉树
- 按照层序遍历的顺序放置节点, 比起满二叉树, 后面可能会空出来几个节点的位置
- 二叉查找树/二叉排序树/二叉搜索树/Binary Search Tree/BST
- 对于任意一个节点, 左<根<右
- 插入: 小于就插左边,大于就插右边, 有可能退化成链表
- 删除:
- 度为0: 直接删除
- 度为>=1: 与其前驱节点交换, 然后删除前驱节点, 直到前驱节点度为0, 直接删除
- 平衡二叉查找树/平衡二叉搜索树/平衡二叉树/Balanced binary search trees/Adelson-Velsky and Landis Tree/AVL树
- 和二叉查找树一样, 左<根<右
- 每个节点左右子树的高度差最多为1
- 插入: 先和BST一样插进去,然后通过旋转调整高度
- 删除: 先和BST一样删除,然后通过旋转调整高度
- 优点: 可以解决二叉查找树退化成链表的问题
- 缺点: 由于旋转的耗时,AVL树在删除数据时效率很低, 在删除操作较多时,维护平衡所需的代价可能高于其带来的好处
- 红黑树
- 满足以下性质的二叉查找树
- 每个节点要么是黑色, 要么是红色
- 根节点是黑色, 叶子节点是黑色
- 每个红色结点的两个子结点一定都是黑色
- 任意一结点到每个叶子结点的路径都包含数量相同的黑结点
- 红黑树靠三种操作保证自平衡:左旋、右旋和变色
- 优点: 与AVL树相比,红黑树并不追求严格的平衡,而是大致的平衡, 只是确保从根到叶子的最长的可能路径不多于最短的可能路径的两倍长, 可以解决平衡二叉查找树维护平衡成本高的问题
- 缺点: 对于数据在磁盘等辅助存储设备中的情况(如MySQL等数据库),红黑树并不擅长,因为红黑树长得还是太高了。当数据在磁盘中时,磁盘IO会成为最大的性能瓶颈,设计的目标应该是尽量减少IO次数;而树的高度越高,增删改查所需要的IO次数也越多,会严重影响性能
- 满足以下性质的二叉查找树
- B树/平衡多路查找树
- m阶B树定义
- 每个结点最多有m-1个关键字。
- 根结点最少可以只有1个关键字。
- 非根结点至少有m/2-1个关键字。
- 每个结点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
- 所有叶子结点都位于同一层,或者说根结点到每个叶子结点的长度都相同。
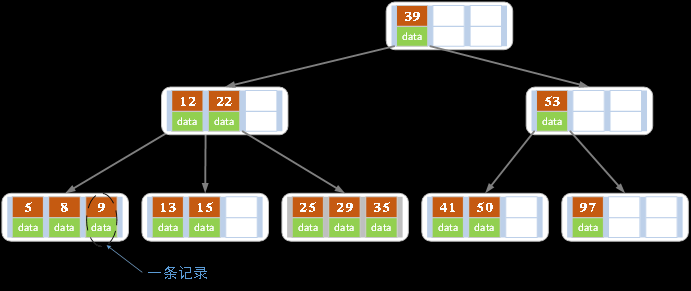
- 如图是一颗阶数为4的B树。在实际应用中的B树的阶数m都非常大(通常大于100),所以即使存储大量的数据,B树的高度仍然比较小. key就表示键,而data表示了这个键对应的条目在硬盘上的逻辑地址
- 优点:
- 由于是多阶的, 树高相比于红黑树更小, 因此磁盘io更少
- B树将键相近的数据存储在同一个节点, 提高缓存的命中率
- 缺点:
- B树的范围查找需要先二分查找到下界, 然后再中序遍历直到上界为止
- IO操作虽然比红黑树少了, 但是比B+树还是多
- m阶B树定义
- B+树
- m阶B+树定义:
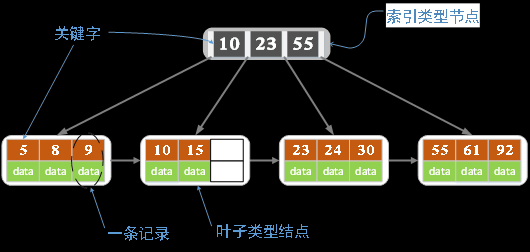
- B+树包含2种类型的结点:内部结点(也称索引结点)和叶子结点。根结点本身即可以是内部结点,也可以是叶子结点。根结点的关键字个数最少可以只有1个。
- B+树与B树最大的不同是内部结点不保存数据,只用于索引,所有数据(或者说记录)都保存在叶子结点中。
- m阶B+树表示了内部结点最多有m-1个关键字(或者说内部结点最多有m个子树),阶数m同时限制了叶子结点最多存储m-1个记录。
- 内部结点中的key都按照从小到大的顺序排列,对于内部结点中的一个key,左树中的所有key都小于它,右子树中的key都大于等于它。叶子结点中的记录也按照key的大小排列。
- 每个叶子结点都存有相邻叶子结点的指针,叶子结点本身依关键字的大小自小而大顺序链接。
- 为什么B+树把叶子节点连起来?
- B+树只有叶结点存储数据。叶结点连起来正好是所有数据的有序序列,可以用来做全表顺序扫描或者范围查询。
- 而B树的数据存储在各层结点上,叶结点只有部分数据,连起来也没有任何用处。
- B+树为什么把数据都放在叶子节点上?
- 树的高度是由阶数决定的,阶数越大树越矮, 而阶数的大小又取决于每个节点可以存储多少条记录, 每个节点占用一个页(4KB), 非叶子节点全部储存key能尽可能让树更矮
- 优点:
- 更少的IO次数:B+树的非叶节点只包含键,而不包含真实数据,因此每个节点存储的记录个数比B数多很多(即阶m更大),因此B+树的高度更低,访问时所需要的IO次数更少。此外,由于每个节点存储的记录数更多,所以对访问局部性原理的利用更好,缓存命中率更高。
- 更适于范围查询:在B树中进行范围查询时,首先找到要查找的下限,然后对B树进行中序遍历,直到找到查找的上限;而B+树的范围查询,只需要对链表进行遍历即可。
- 更稳定的查询效率:B树的查询时间复杂度在1到树高之间(分别对应记录在根节点和叶节点),而B+树的查询复杂度则稳定为树高,因为所有数据都在叶节点。
- 缺点:
- 由于key会重复出现,因此会比B树占用更多的空间
- m阶B+树定义:
key-value 原理