图的java实现
邻接矩阵
如果是无向图,那就在n*n的矩阵里存储0和1即可,代表有边和无边。
如果是有向图,那就在矩阵里存权值,权值为正无穷表示没有相应的边。
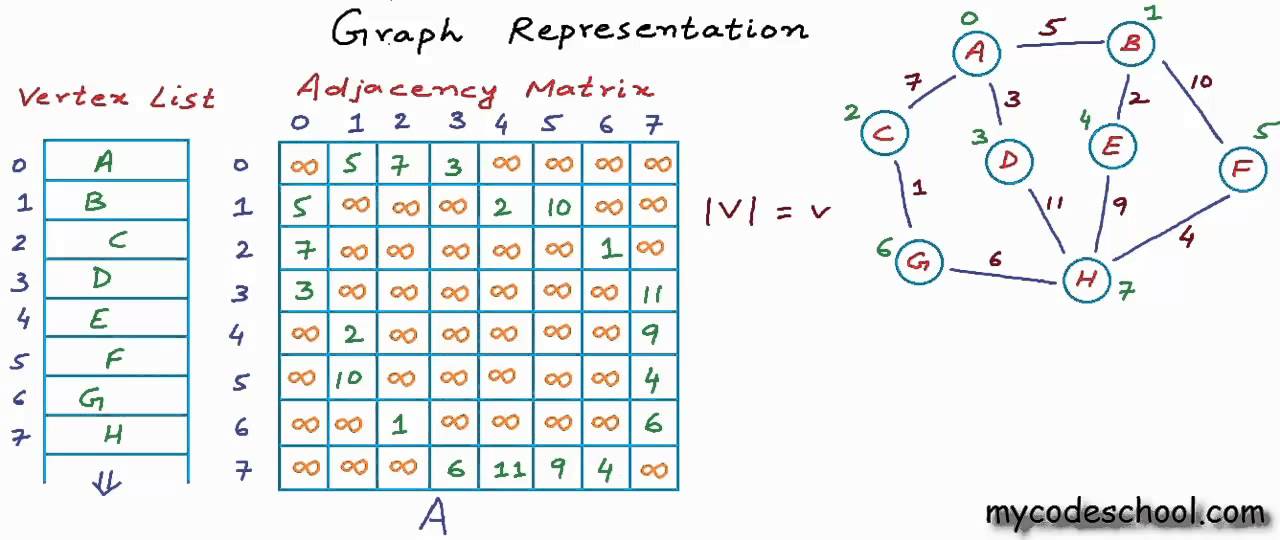
优点:1. 实现简单 2. 可以快速判断两个顶点之间是否存在边 3.可以快速增删边
缺点:如果是稀疏图会比较浪费空间,不适合增删节点
class Graph{
int vexNum;
int edgeNum;
String[] vertices;
int[][] edges;
Graph(int vexNum, int edgeNum, String[] vertices, int[][] edges){
this.vexNum = vexNum;
this.edgeNum = edgeNum;
this.vertices = vertices;
this.edges = edges;
}
}
邻接表
邻接表是由图顶点和边指针构成的数组,可以按照节点标号(下标)快速随机访问,从顶点出发的所有边都被用单链表串起来。
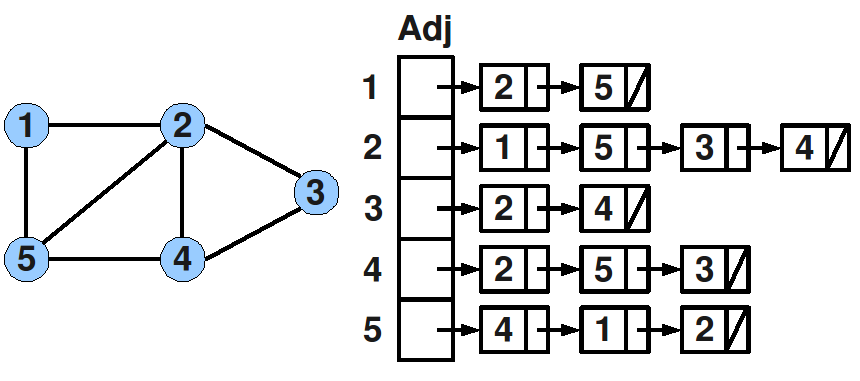
优点:1.存储稀疏图时可以节省空间。 2. 可以动态增删节点
缺点:无法快速判断两个节点是否相邻,增删边比较麻烦
class ArcNode{
int weight; // 边的权重
int vexIndex; // 这条边指向的节点 的编号
ArcNode nextArc; // 下一条边
ArcNode(int weight, int adjVex, ArcNode nextArc){
this.weight = weight;
this.vexIndex = vexIndex;
this.nextArc = nextArc;
}
}
class VNode{
int index; // 节点的编号
String data; // 节点的数据
ArcNode firstArc; // 从这个点出发的第一条边
VNode(int index, String data, ArcNode firstArc){
this.index = index;
this.data = data;
this.firstArc = firstArc;
}
}
class Graph{
int vexNum;
int arcNum;
VNode[] vertices;
Graph(int vexNum, int arcNum, VNode[] vertices){
this.vexNum = vexNum;
this.arcNum = arcNum;
this.vertices = vertices;
}
}
遍历
深度优先遍历
public class Main {
public static void main(String[] args) {
int[][] edges = {
{0, 1, 1, 0},
{1, 0, 1, 0},
{1, 1, 0, 0},
{0, 0, 0, 0}
};
boolean[] visited = new boolean[edges.length];
for (int i = 0; i < visited.length; i++) {
visited[i] = false;
}
for (int i = 0; i < edges.length; i++) {
if(!visited[i]){
traverse(edges, visited, i);
}
}
for (int i = 0; i < visited.length; i++) {
System.out.println(visited[i]);
}
}
static void traverse(int[][] edges, boolean[] visited, int i){
if(visited[i]) return;
visited[i] = true;
System.out.println(i);
for(int j=0; j<edges.length; j++){
if(edges[i][j] != 0){
traverse(edges, visited, j);
}
}
}
}
最短路径
dijkstra算法
dijkstra算法是一种经典的基于贪心的单源最短路算法,其要求图中的边全部非负