常见的排序算法及其Python实现
性能分析
| 方法 | 最好情况 | 最坏情况 | 平均情况 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 直接插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | √ |
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | √ |
| 简单选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | × |
| 希尔排序 | - | - | - | O(1) | × |
| 快速排序 | O(nlogn) | O(n^2) | O(nlogn) | O(logn)~O(n) | × |
| 堆排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(1) | × |
| 归并排序 | O(nlogn) | O(nlogn) | O(nlogn) | O(n) | √ |
| 基数排序 | O(d(n+d)) | O(d(n+d)) | O(d(n+d))) | O(rd) | √ |
算法思想及Python实现
以下所有算法都是在整数组成的列表中进行,下标均从零开始,升序排序。
- 直接插入排序
先把第一个元素看称一个元素组成的有序表,其他元素组成无序表。每次从无序表中取出第一个元素,把它插入到有序表的合适位置,使有序表仍然有序。每一趟使有序表增加一个元素。

def insert_sort(L):
for i in range(1, len(L)):
temp = L[i]
j = i-1
while j>=0 and L[j]>temp:
L[j+1] = L[j]
j -= 1
L[j+1] = temp
- 冒泡排序
从前往后,相邻的两个元素两两进行比较,保证每两个数都是“小,大”,每一趟都可以使一个最大的元素冒到序列最后去,待排序元素个数减一。

def bubble_sort(L):
for i in range(len(L)):
for j in range(len(L) - i - 1):
if L[j] > L[j+1]:
L[j], L[j+1] = L[j+1], L[j]
- 简单选择排序
首先在n个元素中遍历一遍,找到最小的元素,将其放在开头去。然后在剩下n-1个元素中重复此操作。

def selection_sort(L):
for i in range(len(L)):
t = i
for j in range(i, len(L)):
if L[t] > L[j]:
t = j
L[i], L[t] = L[t], L[i]
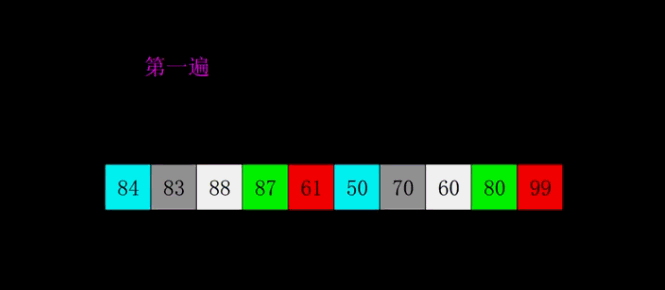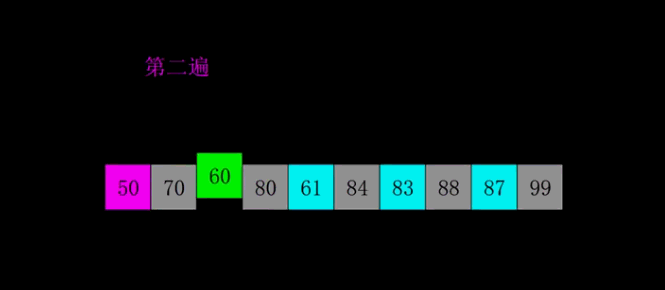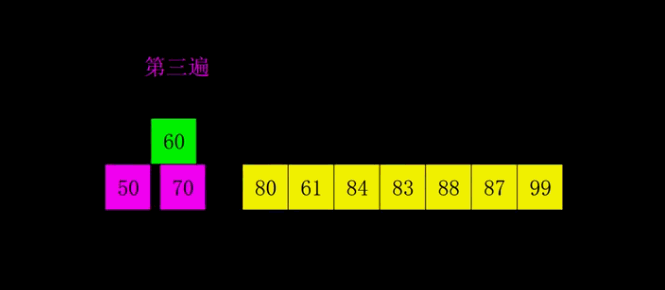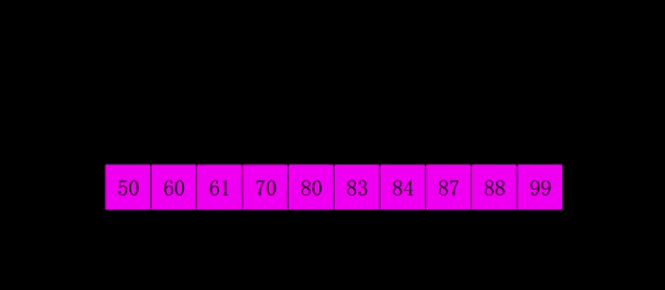
- 希尔排序
又叫“缩小增量排序”,是直接插入排序的改进版,先选择一个较大的步长,进行直接插入排序,然后逐渐缩小步长,直到最后步长为1,再进行直接插入排序,这时候由于序列已经基本有序,所以直接插入排序很快。刚开始选择较长的步长让一个元素可以一次性地朝最终位置前进一大步,因此比直接插入排序表现要好,由此成为历史上第一个突破O(n^2)的排序算法。但步长如何选择为最优至今仍未有定论。
def shell_sort(L):
n = len(L)
gap = n // 2
while gap > 0:
for i in range(gap, n):
temp = L[i]
j = i
while j >= 0 and L[j - gap] > temp:
L[j] = L[j - gap]
j -= gap
L[j] = temp
gap = gap // 2
- 快速排序
又叫分区交换排序,使用分治法策略来把一个序列分为较小和较大的2个子序列,然后递归地排序两个子序列。其中每一次递归的操作是:选定一个枢轴,将小的放左边,大的放右边。递归结束的条件是数组有1个或0个元素。快排思想可用于求大量数据中第k小的元素。
def quick_sort(L):
if len(L) <= 1:
return L
left, right, mid = [], [], []
pivot = random.choice(L)
for number in L:
if number == pivot:
mid.append(number)
elif number < pivot:
left.append(number)
else:
right.append(number)
return quick_sort(left) + mid + quick_sort(right)
- 堆排序
堆:结构近似完全二叉树,子节点的键值或索引总是小于(或者大于)它的父节点。升序排序要建立大顶堆,堆排序是对简单选择排序的改进。堆排序思想可用于求大量数据中的最大或最小的几个。

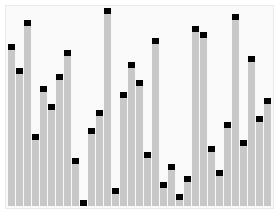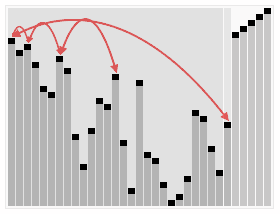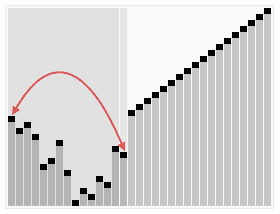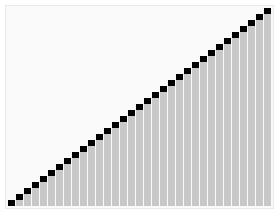
- 归并排序
采用分治法,递归地把当前序列平均分割成两半,然后在保持元素顺序的同时将上一步得到的子序列集成到一起(归并)。

- 基数排序
将整数按位数切割成不同的数字,然后按每个位数分别比较。

